Oscar Dadfar (odadfar) Fall 2020
This project focused on implementing deffered shading into the assignment 1 rasterization pipeline. Our results show that there is an evident trade-off in the speedup of deferring rasterizatin and the penalty of memory accessing in the G-buffer that lead to results that only mearly improve temporal performance in more compelx scenes.
Using Assignment 1 as starter code, I added an extension to the Framebuffer.h class that could append G-buffer data. The following data was stored (adjacent per element):
typedef struct gBufferContent {
bool visited;______//true if needs to be computed
int i;_____________//index into triangle buffer
int triID;_________//unique triangle ID
int t;_____________//thread bucket triangle lies in
float z;___________//depth of shaded pixel (used for z-test)
int type;__________//0-3 indicating what region of the 2x2 SIMD vector
__m128 gamma;______//SIMD vector of gammas
__m128 beta;_______//SIMD vector of betas
__m128 alpha;______//SIMD vector of alphas
int coverage;______//coverage mask of 2x2 SIMD vector
} gBuffer_t;
In TiledRenderer.cpp where the shading instructions originally were, these calls were replaces with calls to store contents to the G-Buffer. Each frame tile had its own G-Buffer so that multiple threads wouldn't have concurrency issues when attempting to write to the same global struct. In each save to the G-Buffer, we would store SIMD-formatted info of the 2x2 region that would later be used to shade, as well as info of which of the 4 fragments in the 2x2 region would use this info. It was very likely along edges that some of the 4 fragments would require info from one triangle, and the other fragments would require info from another. In order to make this easier, the program makes sure that the 2x2 fragments are aligned, meaning that every time a 2x2 SIMD unit comes in, its top left coordinate is even in both the x and y coordinate. A diagram of how the algorithm rasterizes the red primitve can be seen below, where the pink region is the active area that we scan with 2x2 fragment SIMD vectors. We make sure the active area is evenly aligned on the x and y axis so that if SIMD vectors from other areas cross into the red primitive's active area, they will share the same coordinates.

The program continues iterating over all the 2x2 fragment chunks in the tile before shading any of the results. Upon shading, the program iterates through each pixel, and checks if any nearby pixels in a 1 pixel radius share the same triangle (and ultimately same texture). If so, then they are paired together in a SIMD unit and used in the same texture fetch. Thus, for 2x2 fragments completely inside the triangle, we still get the same SIMD execution as the original tiled renderer. It is when each fragment around our current fragment is a different triangle that we need to shade the current fragment individually (thus wasting SIMD units).
The below results were run on a GHC machine with _ cores and _____.
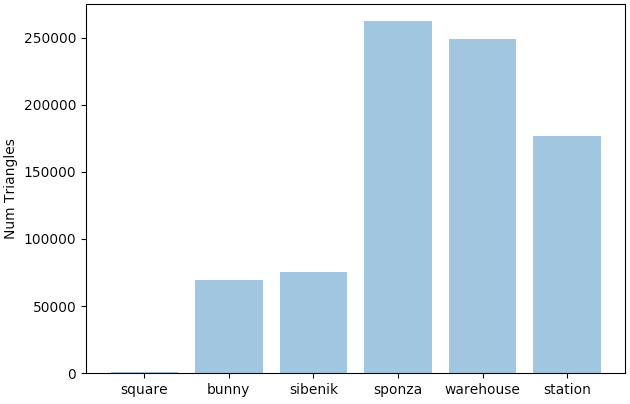
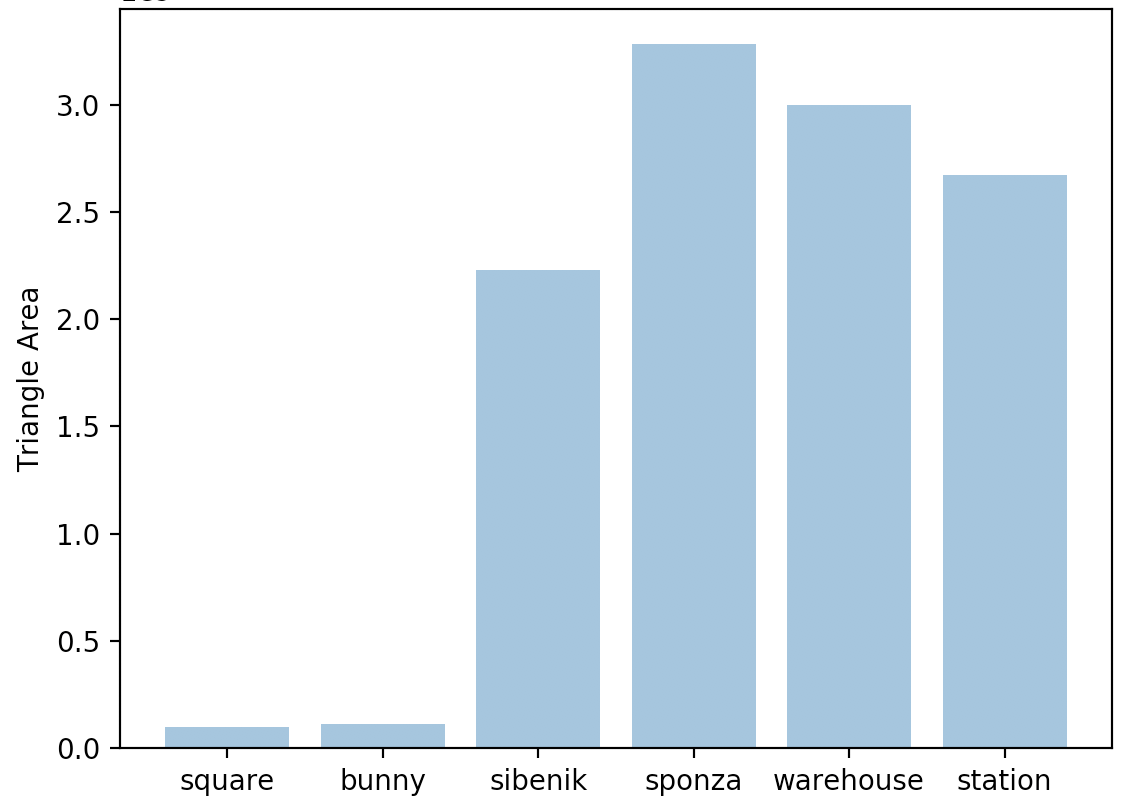
| Scene | Avg Triangle Area (pixel^2) | Num Triangles | Non-Tiled (ms) | Tiled (ms) | Tiled Deffered (ms) |
|---|---|---|---|---|---|
| square | 87,830.28 | 1,152 | 9.7 | 3.5 | 9.2 |
| bunny | 1,644.98 | 69,451 | 23.2 | 11.4 | 20.1 |
| sibenik | 29,593.36 | 75,284 | 61.1 | 26.3 | 27.8 |
| sponza | 12,508.89 | 262,267 | 147.2 | 82.3 | 68.5 |
| warehouse | 12,053.86 | 248,735 | 190.1 | 78.7 | 71.4 |
| station | 15,132.10 | 176,617 | 92.4 | 48.5 | 49.7 |
The above table showcases the temporal results on different scenes. An interesting point to observe is that our tiled deferred renderer performs better only if there is a high primitive count. Each scene was rendered at the same resolution (1024x768), so higher primitive counts direclty led to more overlap in primitives. This means that scenes with more overlap were more likely to do uneccessary shading in the non-deferred case that we were able to avoid (and cut down time on) in the defferred case. Otherwise, if there is a lack of significant overlap in the primitives, then our overhead for creating and storing/reading from the G-Buffer outweight the temporal gain we get from deferring shading, thus leading to higher deferred times than in the non-deffered case.